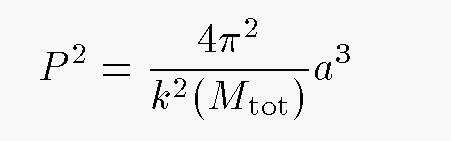Las leyes de la naturaleza se describen mediante ecuaciones, pero para encontrarlas a menudo hay que pensar fuera de las matemáticas, ¿puede hacerlo también una inteligencia artificial?
El pasado mes de abril un artículo científico publicado en Nature provocó un buen número de titulares sensacionalistas, como por ejemplo que «una nueva IA piensa igual que los científicos más famosos», o «una IA hace los mismos descubrimientos que Kepler y compañía».
¿Qué hacen los científicos? Parten de principios conocidos e infieren las leyes de la naturaleza, es decir, reglas que pueden aplicarse de modo general, como las ecuaciones de la física (y supuestamente, la inteligencia artificial). Descartes pudo «descubrir» la tercera ley de Kepler, que es la que rige el periodo de los planetas en su órbita alrededor del sol. ¿Lo hizo? La ecuación descubierta por Kepler aplicada a la Tierra y el Sol es esta:
Donde P es el periodo del planeta, a el tamaño de la órbita del planeta, es decir, el semieje mayor de la elipse, M la suma de la masa del Sol y la Tierra, y k la constante gravitacional gaussiana.
Si embargo, el valor de P según la ecuación de la tercera ley de Kepler «descubierta» por la IA fue esta:

Donde d=a. Esto no se parece en nada a lo que podríamos recordar de las clases de la escuela. Allí, normalmente aprendemos sobre la tercera ley de Kepler del movimiento planetario de esta forma: «Los cuadrados de los períodos orbitales están en la misma proporción que los cubos de los semiejes mayores de la elipse».
El cuadrado del período orbital (p) y la tercera potencia de la distancia del planeta al Sol (d) pueden verse sin duda en la fórmula. Sin embargo, la ecuación de la IA tiene poco que ver con la tercera ley de Kepler tal y como la conocemos normalmente. En su forma exacta, hay que tener en cuenta, por supuesto, la masa del Sol y de los planetas que lo habitan, así como la constante gravitatoria. Las masas, la constante gravitatoria y otros factores numéricos de la fórmula de Kepler pueden considerarse resumidos en el número 0,1319 (y aún hay que tener en cuenta que, por razones técnicas, la IA no calculó con las unidades habituales del SI de metro, kilogramo y segundo). Pero esta ecuación dista mucho de ser una verdadera «ley de la naturaleza» o una intuición que se acerque a la de Johannes Kepler.
Una IA no puede equipararse a Kepler o Newton
Esto ya empieza con los requisitos previos: la inteligencia artificial no sólo recibió datos sobre masas, distancias y períodos orbitales, sino también diversas fórmulas, incluida la ley de la gravedad de Newton. A diferencia de Johannes Kepler, la IA ya «sabía» cómo se atraen los cuerpos celestes. Si Kepler hubiera poseído este conocimiento, podría haberse ahorrado el trabajo con sus tres leyes, pues no son más que otra formulación de lo que Isaac Newton descubrió más tarde (y con mucha más precisión). A la fórmula que desarrolló para la conexión entre periodo orbital y distancia también le falta parte de su contenido físico. Precisamente porque no se enumeran explícitamente factores como la constante gravitatoria o las masas implicadas, es casi imposible deducir más conclusiones de ella.
La inteligencia artificial ha ideado otras fórmulas, algunas de las cuales también tienen en cuenta las masas. Sin embargo, esto tiene poco que ver con lo que haría un humano con los datos. Para ello, basta con echar un vistazo a la «Astronomia Nova». En esta obra del siglo XVII, Kepler anotaba, casi a modo de diario, el proceso creativo que finalmente condujo a sus descubrimientos. La IA, por su parte, solo ha encontrado una fórmula útil para describir los datos observacionales. Esto también es un logro relevante: el nuevo trabajo ha demostrado que se puede conseguir que una IA formule relaciones matemáticas medianamente significativas. Pero eso no tiene nada que ver con «pensar como los científicos más famosos».
REFERENCIA
Combining data and theory for derivable scientific discovery with AI-Descartes